Esta publicação será tratada em duas partes. Nesta primeira parte vamos falar a respeito de alguns dos algoritmos de ordenação mais populares, comentar sua estrutura e falar um pouco sobre as complexidades de algoritmo. Já na segunda parte, vamos realizar uma análise (benchmark) entre eles para comparar performance e ter alguns dados mais concretos. Serão comparados os algoritmos de ordenação: Bubblesort, Heapsort, Quicksort e Radixsort. Faremos esta análise utilizando a linguagem de programação Python. Lembrando que este tipo de análise pode variar de acordo com o hardware empregado, linguagem utilizada entre outros fatores.
Informalmente, um algoritmo é qualquer procedimento computacional bem definido que toma algum valor ou conjunto de valores como entrada e produz algum valor ou conjunto de valores como saída. Analisar um algoritmo significa prever os recursos de que o algoritmo necessitará. Ocasionalmente, recursos como memória, largura de banda de comunicação ou hardware de computador são as principais preocupações, mas com frequência é o tempo de computação que desejamos medir e é o que levaremos em consideração.
Agora que já sabemos quais algoritmos de ordenação serão analisados, qual a definição de algoritmo e o que é uma análise de algoritmos, vamos conhecer sobre os algoritmos de ordenação e analisá-los.
Algoritmos de Ordenação
Bubblesort
Por sua simplicidade de entendimento e fácil implementação, o bubblesort está entre os mais conhecidos e difundidos algoritmos de ordenação. Porém, por não se tratar de um algoritmo eficiente, é mais utilizado para estudos e desenvolvimento de raciocínio lógico.
O princípio do bubblesort é a troca de valores entre posições adjacentes (valores lado a lado) numa lista de N elementos, fazendo com que os valores mais altos sejam transportados para o final do vetor (no caso de uma ordenação crescente). Este processo pode se repetir N vezes, até que o vetor esteja completamente ordenado. A versão otimizada do bubblesort decrementa o tamanho do vetor, uma vez que os maiores elementos de cada loop estarão obrigatoriamente no final e através de um operador booleano, garante que não haverá loops desnecessários caso o vetor já esteja ordenado.
Não é difícil identificar que seu tempo de execução no pior caso e de caso médio é O(n²), pois na média é necessário percorrer o vetor de N elementos, N vezes (N-K vezes), para fazer a ordenação (N*N = N²). Já para o melhor caso é O(n) e, neste momento, você já deve conseguir imaginar um exemplo. Caso tenha uma lista previamente ordenada.
Simuladores: Universidade São Francisco; VisuAlgo.
Atenção: fuja de algoritmos de complexidade O(n²) ou piores, principalmente se a quantidade de elementos da sequência for grande. 😛
def optimizedBubblesort(v):
update = True
n = len(v)
while update is True and n > 1:
update = False
for i in range(n - 1):
if v[i] > v[i + 1]:
v[i], v[i + 1] = v[i + 1], v[i]
update = True
n -= 1
return v
Heapsort
O heapsort é um algoritmo de ordenação baseado numa estrutura de dados conhecida como Heap, muito útil na construção de filas de prioridade. Heaps são Árvores Binárias Completas que devem respeitar algumas propriedades. Em um heap, cada nodo pai possui no máximo dois filhos, até o seu penúltimo nível deve ter o máximo de elementos possível e o último nível, se não estiver completo, deve ter seus elementos agrupados a esquerda. Imagine uma árvore de nível h = 3 (altura 4), onde o nível zero é o nodo raiz. Nesta situação, os níveis 0, 1 e 2 precisam estar completos, ou seja, ter o maior número de nodos possível, o que resultaria em no mínimo 7 elementos (20 +2¹ + 2² = 7). Há dois tipos de Heap: Max Heap, onde os nodos filhos são sempre menores que o nodo pai e o Min Heap, que os filhos são sempre maiores que o pai, resultando em árvores com maior (ou menor) elemento na raiz dependendo da implementação. Árvores são estruturas de dados bem interessantes e com ótima performance, voltaremos a falar sobre o assunto em um tópico dedicado.
A execução do algoritmo heapsort é interessante. Pode-se separar o algoritmo em duas fases: Na primeira fase, a qual é chamada de heapfy, constrói-se a estrutura de árvore heap no arranjo utilizando uma técnica de execução que vai de baixo para cima (Botton-up). Esta técnica identifica através do número de elementos 'N' do arranjo, quem é o nodo pai do último nó folha da árvore. Em seguida, é verificado se algum dos filhos é maior que o nó pai. Se for, o nodo pai troca de posição com o maior filho, num processo conhecido como down heap (sucessivamente caso tenha mais filhos abaixo). Repete-se este processo até completar a construção da árvore e ajustar sua propriedade de Max Heap (neste caso). Agora que o heap está construído com o maior elemento no topo, inicia-se a segunda fase, onde é feito a troca de posição do maior elemento com o elemento da última posição do arranjo. Como a propriedade da árvore pode ter sido quebrada, então aplica-se novamente o downheap para garantir que suas propriedades sejam respeitadas. Este processo é repetido até que o vetor seja completamente ordenado.
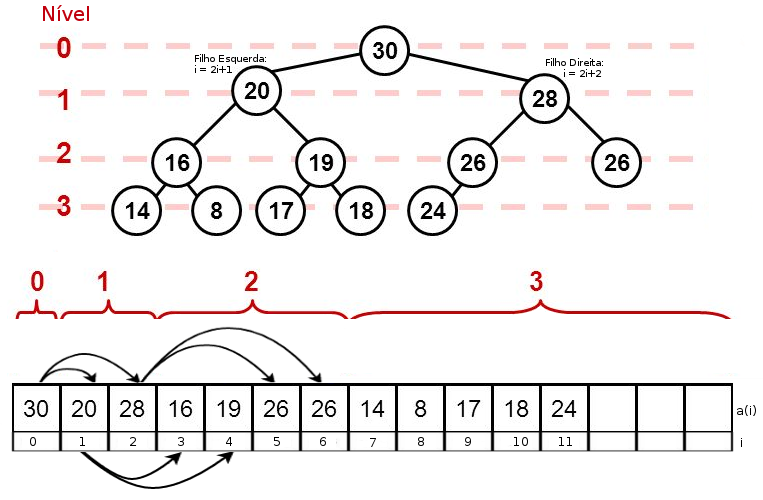
Representação em Array de Árvore Binária Completa
O tempo de execução para conjuntos de N elementos ordenados aleatoriamente em árvores heap é muito bom, com desempenho no melhor cenário, cenário médio e no pior cenário praticamente igual. Estamos falando de um algoritmo de ordenação em tempo logarítmico, ou seja, O(n log n). Para valores de N razoavelmente grandes, o termo 'log n' é quase constante, de modo que o tempo de ordenação se aproxima de tempo linear. É importante saber que sempre que citarmos a operação log, estamos referindo ao log na base 2, ou O(n log 2 n). Em projetos de tempo real, onde deve-se ter garantia de tempo para executar determinadas operações, o heapsort é uma ótima escolha.
Simulador: Universidade São Francisco.
def heapsort(v):
def downHeap(start, end):
parent = start
while True:
leftChild = parent * 2 + 1
rightChild = parent * 2 + 2
biggestChild = leftChild
if leftChild > end: break
if rightChild <= end and v[leftChild] < v[rightChild]: biggestChild = rightChild
if v[parent] < v[biggestChild]:
swap(parent, biggestChild)
parent = biggestChild
else:
break
def swap(pos1, pos2):
v[pos1], v[pos2] = v[pos2], v[pos1]
# Heapfy - Faz a contrução botton-up do heap
lastParent = (len(v) - 2) / 2
end = len(v) - 1
for start in range(lastParent, -1, -1):
downHeap(start, end)
# Passa o maior elemento para o final, decrementa o vetor e reestrutura com downheap
lastIndex = len(v) - 1
for end in range(lastIndex, 0, -1):
swap(end, 0)
downHeap(0, end - 1)
return v
Quicksort
O quicksort é um clássico dos algoritmos de ordenação, até mesmo fazendo parte das bibliotecas da linguagem C. Assim como o heapsort, ele também é estruturado como uma Árvore Binária. Sua estratégia de ordenação é baseada no padrão de projeto (Design Pattern) divisão e conquista, utilizando como parte da estratégia a recursividade.
A execução do quicksort consiste em dividir uma sequência em subsequências menores recursivamente. Primeiro, é escolhido um elemento qualquer da sequência como referência, o qual é chamado de pivô (pivot). Geralmente escolhe-se o primeiro ou o último elemento da sequência, evitando o tempo de processamento da escolha aleatória. Em seguida, ordena-se os elementos em subsequências com os elementos menores à esquerda (left) e os elementos maiores a direita (right) através da recursão e, finalmente, concatenando as subsequências ordenadas até obter a lista ordenada.
O algoritmo quicksort consome tempo proporcional a O(n log n) em média, em geral é muito rápido. Porém, em algumas raras instâncias ele pode ser tão lento quanto os algoritmos elementares, com tempo de execução de O(n²) no pior caso. Por esta razão não é recomendado utilizar o quicksort em projetos de tempo real. É possível eliminar essa situação de pior caso O(n²) com a versão randomizada do quicksort. A versão randomizada utiliza um pivô aleatório ao invés de utilizar um índice fixo do início ou final do arranjo, com isso obtendo na ordem de pior caso O(n long n).
Simuladores: Universidade São Francisco; VisuAlgo.
def quicksort(v):
if len(v) > 1:
pivotIndex = len(v) - 1
# Arrays auxiliares
pivot = [v[pivotIndex]]
elements = v[:pivotIndex]
left, right = [], []
# Divisão
for element in elements:
if element < pivot[0]:
left.append(element)
else:
right.append(element)
# Recursão
left = quicksort(left)
right = quicksort(right)
# Conquista
return left + pivot + right
return v
Radixsort
O radixsort é um algoritmo de ordenação rápido e estável, que pode ser usado para ordenação baseado no uso de chaves como índice ao invés de utilizar a comparação de elementos conforme visto nos demais algoritmos. Esta característica o torna aplicável em um contexto mais amplo do que a ordenação de valores inteiros, por exemplo. Por ser um algoritmo estável, é possível realizar a ordenação de elementos de forma lexográfica, ou seja, apresentar uma ordenação da mesma forma que um dicionário (bala, bolo, brigadeiro... uhnn 😛 ). Obs: A versão apresentada abaixo é para ordenação numérica apenas.
A ordenação do radix é feita através de cada componente de uma palavra (ou número), e não da palavra como um todo, por esta razão não é necessário fazer as comparações. Sua execução Inicia-se pelo último componente de cada elemento do arranjo, seguindo sucessivamente até o primeiro componente. É necessário respeitar essa ordem para realizar a ordenação lexográfica da sequência. O algoritmo utiliza um vetor auxiliar e usa seus índices como "baldes" (buckets) para inserir cada elemento da sequência de acordo com a verificação da componente em análise. Após passar por todos os elementos da lista fazendo esse processo para a última componente, retira-se os elementos dos "baldes" em ordem os colocando-os de volta na lista. Então reinicia o processo, porém desta vez para a penúltima componente de cada elemento, até que termine a verificação de todos 'K' componentes. Logo para uma palavra de 4 letras, seria repetido o processo 4 vezes. Para ficar mais claro o que tratamos como elemento e componente, image o vetor a = [0, 20, 300]. 300 é um elemento e 3, 0 e 0 são os componentes que formam o elemento 300.
O fato de não ser necessário fazer comparações entre os elementos, rompe-se um limite inferior de tempo de ordenação, que é de O(n log n), conforme vimos nos algoritmos heapsort e quicksort. A complexidade computacional do radisort é da ordem de O(kn), onde 'K' é o tamanho da maior palavra e 'N' o número de elementos para ordenação , sendo então de complexidade temporal linear, O(n). Porém, isso não significa que ele é sempre a melhor opção para todas as situações, conforme veremos abaixo.
Simuladores: Universidade São Francisco; VisuAlgo.
def radixsort(v):
RADIX_DECIMAL = 10
maxLength = False
tmp, placement = -1, 1
while not maxLength:
maxLength = True
# Inicializa a lista com a qtde de baldes necessarios
# Obs: Ordenacao de numeros decimais, necessário apenas 10 posições (0,1,...,8,9).
buckets = [ list() for _ in range(RADIX_DECIMAL) ]
# Separa cada elementos em seu respectivo balde
for e in v:
tmp = e // placement
bucketPos = tmp % RADIX_DECIMAL
buckets[bucketPos].append(e)
# se tmp = 0, então todos digitos foram percorridos
if maxLength and tmp > 0:
maxLength = False
i = 0
# Percorre a lista de baldes, pegando os elementos de cada balde e adicionando no vetor para reiniciar ordenacao
for bucket in buckets:
for e in bucket:
v[i] = e
i += 1
# Vai para o próximo digito. Ex: 10, 100, 1000...
placement *= RADIX_DECIMAL
return v
Fonte do Algoritmo: http://www.geekviewpoint.com/python/sorting/radixsort
Após analisar a estrutura dos algoritmos de ordenação citados acima e suas complexidades utilizando a notação Big O, você deve estar se perguntando: qual deles é o melhor de todos, afinal? Talvez tenha chegado a conclusão de que o radixsort é o melhor algoritmo de ordenação, afinal sua análise de pior caso é O(n), superando os algoritmos bubblesort, heapsort e quicksort, que são baseados em comparação. Na verdade, não existe um algoritmo de ordenação melhor que todos. Cada algoritmo irá se comportar melhor em um determinado cenário, por isso é muito importante levar em consideração a análise de complexidade conforme vimos ao longo do texto.
Certamente o algoritmo de ordenação com desempenho O(n²), como o bubblesort e outros de desempenho similar, como o selectionsort e insertionsort, são de fato escolhas pobres, pois pode-se obter resultados melhores com algoritmos extremamente simples e eficientes, como o quicksort, por exemplo. No entanto, mesmo que os algoritmos O(n²) sejam lentos, ainda assim podem ser mais rápidos que o próprio radixsort, caso tenhamos um vetor de poucos elementos (25, 30 elementos, por exemplo), porém com números na casa dos milhões, ou seja, que possuem muitos componentes (dígitos).
Esta noção fica muito clara também quando precisamos aplicar um algorítimo de ordenação em um projeto de tempo real. Neste tipo de projeto é necessário finalizar uma determinada operação em um tempo predeterminado e mesmo que os algoritmos heapsort e quicksort tenham performance similares, escolher o quicksort seria um erro de projeto, pois este algoritmo tem complexidade de pior caso O(n²), ainda que em geral seja O(n log n), assim como o heapsort.
Na segunda parte deste artigo faremos uma comparação entre estes algoritmos de ordenação, montando um quadro comparativo entre eles para ver na prática a performance de cada algoritmo. Até breve.

Referências:
- GOODRICH, M.; TAMASSIA, R. Estrutura de dados e algoritmos em Java. Bookman.
- Complexidade de algoritmos: https://www.ime.usp.br/~song/mac5710/slides/01complex.pdf

rodrigo
Paulo Cezar